Questões sobre Números reais e complexos
Lista completa de Questões sobre Números reais e complexos para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Sabendo que o polinômio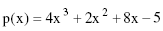 
tem o número complexo 
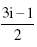como uma de suas raízes, então a soma de todas as raízes de p(x) é igual a
- A.
- B.
- C.
0
- D.
- E.
Seja r um número real positivo, e a, um número complexo. Então o lugar geométrico representado pelo conjunto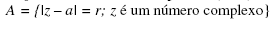 
é uma
- A. circunferência.
- B.
elipse.
- C.
hipérbole.
- D.
parábola.
- E. reta.
Das afirmações abaixo, assinale a verdadeira.
- A.
O produto de dois números racionais pode não ser racional.
- B.
O produto de dois números irracionais pode não ser irracional.
- C.
O produto de um número racional não-nulo com um irracional pode não ser irracional.
- D.
O produto de dois números ímpares pode não ser ímpar.
- E.
O produto de um número ímpar com um número primo é sempre ímpar.
Seja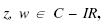 
conjunto dos números complexos que não são reais. Se 
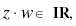então podemos sempre afirmar que
- A. z = w
- B.
z é o conjugado de w
- C.
z . w = 1
- D.
- E.
NAS QUESTÕES NUMERADAS DE 16 A 40, ASSINALE A ÚNICA ALTERNATIVA QUE RESPONDE CORRETAMENTE AO ENUNCIADO.
Dados o conjunto C dos números complexos, as operações usuais de adição (+) e de multiplicação (x) de números complexos e multiplicação de número complexo por um escalar real (λ), é correto afirmar que:
- A.
(C, λ ) é um grupo comutativo.
- B.
(C, +, λ ) é um grupo comutativo.
- C.
(C, x, λ) é um espaço vetorial.
- D.
(C, +, x) é um anel.
Considerando como universo o conjunto dos reais maiores que ou iguais a zero, analise os itens a seguir.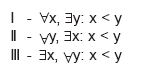 
- A.
I, apenas.
- B.
II, apenas.
- C.
I e III, apenas.
- D.
II e III, apenas.
- E.
I, II e III.
Matemática - Números reais e complexos - Fundação para o Vestibular da Universidade Estadual Paulista (VUNESP) - 2006
Pode-se afirmar que o simétrico e o módulo de –6 são, respectivamente:
- A.
6 e –6.
- B.
–6 e 6.
- C.
6 e 1/6.
- D.
–1/6 e 6.
- E.
6 e 6.
Indique qual dos números abaixo é um número irracional.
- A.
0
- B.
0,5
- C.
0,33...
- D.
1/3
- E.
que mede a razão entre o comprimento da circunferência e o seu diâmetro.
Matemática - Números reais e complexos - Pontifícia Universidade Católica do Paraná (PUC - PR) - 2006
Considerando o conjunto dos números inteiros Z = { ..., -2, -1, 0, 1, 2, .....}, analise as afirmações a seguir:
I) (-2). (+1).(-3) - 21:7 , é um número inteiro positivo.
II) O número 4/5 não é um número inteiro.
III) 25 , é um número inteiro positivo.
- A. I ,II e III são verdadeiras.
- B. I e III são verdadeiras.
- C. II e III são verdadeiras.
- D. I e II são verdadeiras.
- E. I,II e III são FALSAS.
No conjunto Z dos inteiros, considere as seguintes afirmações:
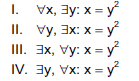
O número de afirmações verdadeiras é:
- A.
0
- B.
1
- C.
2
- D.
3
- E.
4
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
