Questões sobre Distribuição t de Student

Um banco deseja testar se a produtividade média de um grupo de empregados de determinado setor da agência I é igual à produtividade média de um outro grupo de empregados de um setor equivalente da agência II. A produtividade foi definida em função do número diário de contratos avaliados por cada empregado. Como as duas agências possuem características similares, foram coletadas amostras de igual tamanho (32 empregados), obtendo-se os resultados apresentados na tabela a seguir. Considere que as distribuições das produtividades de ambas as agências sejam normais com variâncias iguais.

Considere ainda que o teste t para a comparação da média de duas amostras independentes tenha sido aplicado. Dado que P(Z > 1,96) = 0,025 e P(Z > 2,326) = 0,01, em que Z é uma distribuição normal padrão, julgue os itens a seguir com base nessas informações.

Se a versão do teste t para a comparação entre duas populações independentes com variâncias desiguais fosse aplicada, então a estatística do teste resultaria em um valor superior a 2,2.

• C. Certo
• E. Errado

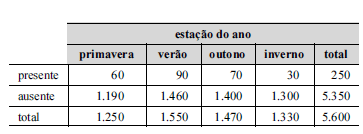
Um dos critérios para a avaliação da qualidade da água para o consumo humano é a detecção de coliformes fecais na água distribuída à população. A tabela acima apresenta os resultados das análises de 5.600 amostras de água coletadas, entre os anos de 1995 a 2000, em uma grande cidade, conforme as estações do ano.

Considerando as informações da tabela acima, julgue os itens a seguir.

Para testar se a distribuição dos resultados das análises das amostras de água é a mesma para todas as estações do ano, é conveniente a aplicação do teste t de Student.

• C. Certo
• E. Errado

Para testar H₀: µ 5 versus H₁: µ > 5, em que µ representa a média de uma distribuição normal com parâmetros desconhecidos, foi usada uma amostra aleatória simples de tamanho 16, que forneceu as seguintes estatísticas:

O p-valor associado à estatística de teste usual, que tem distribuição t-Student quando µ = 5, é tal que:

• A. p < 0,001;
• B. 0,001 < p < 0,025;
• C. 0,025 < p < 0,05;
• D. 0,05 < p < 0,10;
• E. p > 0,10.

Uma revenda de automóveis vende carros montados no Brasil. O proprietário está interessado em estimar o valor médio θ dos gastos extras com opcionais casados com a compra de carros novos. Uma amostra de 16 vendas produziu um valor médio de R$1.062,00 com desvio padrão de R$ 144,00. Assinale a opção que dá os limites de confiança para θ com coeficiente de 98%. A tabela abaixo dá os quantis x , de ordem γ , 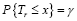 , da distribuição T de Student com r graus de liberdade.

Despreze centavos.

• A.

  [R$ 955,00; R$ 1.168,00]

• B.

  [R$ 968,00; R$ 1.155,00]

• C.

  [R$ 990,00; R$ 1.134,00]

• D.

  [R$ 997,00; R$ 1.124,00]

• E.

  [R$ 938,00; R$ 1.186,00]

Considere o teste da hipótese H : μ =100 contra alternativa A : μ ≠ 100 em uma amostra da normal com média μ e variância σ2. O valor da estatística teste t com distribuição de Student sob a hipótese H : μ =100 é de –1,7864 e sabe-se que P(t≥1,7864)=0,0446.Suponha que a probabilidade de erro do tipo I esteja sendo controlada em 5%. Assinale a resposta correta.

• A.

  Como o valor probabilístico do teste é 0,0446 conclua H :μ = 100.

• B.

  Como o valor probabilístico do teste é 0,0446 conclua A:μ ≠ 100.

• C.

  Como o valor probabilístico do teste é 0,0892 não há evidência para rejeitar H :μ = 100.

• D.

  Como o valor probabilístico do teste é 0,0223 conclua A:μ ≠ 100.

• E.

  Não se pode tirar nenhuma conclusão pois, o tamanho da amostra, a média amostral e o desvio padrão amostral não foram dados.

Nos problemas de estimativa de média utiliza-se a variável " t " de Student quando:

• A. a distribuição original é normal, o desvio padrão da população é conhecido e o tamanho da amostra é inferior a 30.
• B.

  a distribuição original não é normal, o desvio padrão da população é conhecido e o tamanho da amostra é inferior a 30.

• C.

  a distribuição original é normal, o desvio padrão da população é desconhecido e o tamanho da amostra é inferior a 30.

• D.

  a distribuição original é normal, o desvio padrão da população é conhecido e o tamanho da amostra é superior ou igual a 30.

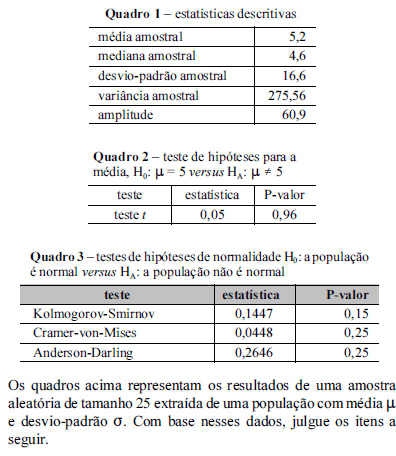
Se a população for normal, então a distribuição amostral da média é t de Student com n -1 graus de liberdade.

• C. Certo
• E. Errado

Em relação ao experimento descrito acima, julgue os itens subseqüentes.

O melhor método estatístico para se comparar as médias do ED50 obtidas nos 4 grupos é o teste T de Student. A análise de variância poderia ser utilizada, caso fossem comparadas duas drogas.

• C. Certo
• E. Errado

A estatística é importante ferramenta para várias áreas do conhecimento, como biologia, química, meio ambiente, física, psicologia, engenharia e várias outras, usada para estimar a confiabilidade dos dados. Os métodos estatísticos e probabilísticos permitem que analistas façam julgamentos com mais segurança. Julgue os itens subseqüentes, que se referem à probabilidade e à estatística.

O teste t de Student é indicado para pequenas amostras, por meio da comparação entre a média e o valor-padrão em um nível de confiança associado.

• C. Certo
• E. Errado

A estatística é importante ferramenta para várias áreas do conhecimento, como biologia, química, meio ambiente, física, psicologia, engenharia e várias outras, usada para estimar a confiabilidade dos dados. Os métodos estatísticos e probabilísticos permitem que analistas façam julgamentos com mais segurança. Julgue os itens subseqüentes, que se referem à probabilidade e à estatística.

As tabelas de distribuição de t fornecem os valores com variados graus de liberdade.

• C. Certo
• E. Errado