Questões sobre Equações Exponenciais
Lista completa de Questões sobre Equações Exponenciais para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
O máximo valor de y = x.e−x (x real) é:
- A.
2e-²
- B.
e-¹
- C.
1
- D.
e
- E.
e²
A população de uma cidade aumenta segundo a equação N = 30 000(1,01)t, onde N é o número de habitantes e t é o tempo em anos. O valor de t para que a população dobre em relação a hoje é de
- A.
- B.
- C.
- D.
- E.
50
Considerando-se que a produção do ano de 2006 seja de p barris anuais de petróleo, a produção de 2010 será:
- A.
p +(0,09)4
- B.
p ⋅(0,09)4
- C.
p +(1,09)4</SUP
- D.
p ⋅(1,09)4
- E.
p +(1,90)4
O número de soluções reais da equação 3x+2 - 3x+3 - 3x + 3 = 0 é igual a:
- A.
0.
- B.
1.
- C.
2.
- D.
3.
- E.
4.
Atualmente, sabe-se que certas bactérias podem facilitar a vida de outros seres como, por exemplo, no auxílio de limpeza das praias, na fabricação de medicamentos, na purificação da água, etc. A tabela abaixo mostra a observação feita em uma cultura de bactérias, a cada meia hora:
- A. 1.024
- B. 2.048
- C. 4.096
- D. 8.192
Os valores da função exponencial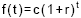 
, t real , c>0 e 1+r>0, nos pontos em que t é um número natural, constituem uma progressão geométrica. Indique a razão desta progressão.
- a.
c.
- b.
1+r.
- c.
c-1.
- d.
r.
- e.
c(1+r).
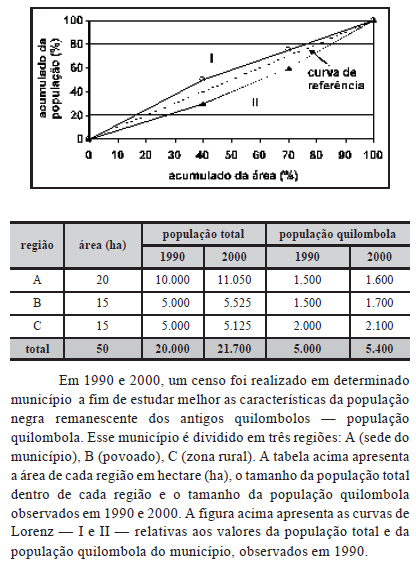
Com relação à situação apresentada acima e acerca da demografia e dos indicadores demográficos, julgue os itens a seguir.
- C. Certo
- E. Errado
Um relatório elaborado pela CODESA estima que, daqui a t anos, estará circulando pelo interior da área portuária N veículos.
Se
, daqui a 8 anos estará circulando a seguinte quantidade de veículos:
- A.
5No
- B.
4N0
- C.
3No
- D.
2No
- E.
No
Matemática - Equações Exponenciais - Fundação de Estudos e Pesquisas Sócio-Econômicos (FEPESE) - 2005
Num período prolongado de seca, a variação da quantidade de água de um certo reservatório é dada pela função q(t) = qo·2(-0,1)t sendo qo a quantidade inicial de água no reservatório e q(t) a quantidade de água no reservatório após t meses.
Em quantos meses a quantidade de água do reservatório se reduzirá à metade do que era no ínicio?
- A.
10
- B.
9
- C.
8
- D.
7
- E.
5
Suponha que uma certa máquina agrícola sofra uma desvalorização de 20% ao ano. Em quanto tempo, aproximadamente, o valor dessa máquina se reduzirá a 10% do valor inicial?
(Use log 2 = 0,30)
- A.
5 anos.
- B.
12 anos.
- C.
8 anos.
- D.
7 anos.
- E.
10 anos.
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
