Questões de Estatística do ano 2013

A tabela a seguir apresenta algumas estatísticas descritivas do “peso” e do “comprimento” de 20 sapos.

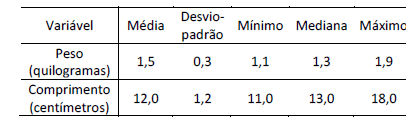
É correto afirmar que os sapos têm

• A. menor variabilidade no “peso” do que no “comprimento”, pois a variância do “peso” é menor que a variância do “comprimento”.
• B. menor variabilidade no “peso” do que no “comprimento”, pois a variância do “peso” é menor que a variância do “comprimento”.
• C. menor variabilidade no “peso” do que no “comprimento”, pois a amplitude total do “peso” é menor que a amplitude total do “comprimento”.
• D. menor variabilidade no “peso” do que no “comprimento”, pois a amplitude total do “peso” é menor que a amplitude total do “comprimento”.
• E. maior variabilidade no “peso” do que no “comprimento”, pois a diferença absoluta entre a média e a mediana é menor no “peso” e menor que no “comprimento”.

É correto afirmar que, no teste de hipóteses para comparar duas médias populacionais,

• A. os erros tipo I e tipo II são eventos complementares.
• B. quanto maior o nível de significância, maior será o valor – p.
• C. o poder do teste aumenta com a redução do tamanho da amostra.
• D. quanto menor o tamanho da amostra, menor será o nível de significância.
• E. o poder do teste aumenta com o aumento da diferença entre as médias populacionais.

Considere o teste T para testar a hipótese nula de que μ, a média de uma variável aleatória com distribuição Normal, seja igual a 0 (zero), usando o nível de significância igual a 0,05. É INCORRETO afirmar que

• A. o poder do teste é maior que 0,05 se μ for igual a 2 (dois).
• B. o cálculo do valor – p depende da definição da hipótese alternativa.
• C. a hipótese nula deve ser rejeitada se o valor – p for menor que 0,05.
• D. a estatística de teste tem distribuição T-de-Student com n graus de liberdade.
• E.

• A.
• B.
• C.
• D.
• E.

Desejando estimar o salário médio dos gerentes de agências bancárias, certo pesquisador tomou uma amostra aleatória simples sem reposição de gerentes, na qual os salários apresentaram média igual a 3,6 mil reais e desvio-padrão igual a 0,5 mil reais. O pesquisador sabe que, na sua população de gerentes, o tempo médio de experiência no cargo é igual a 12 anos, enquanto que, na sua amostra, o tempo médio de experiência no cargo encontrado foi de 8 anos. Sabendo-se da forte relação linear entre o salário e o tempo de experiência no cargo, o pesquisador decidiu usar um estimador de regressão para o salário médio. Para tanto, ajustou nos dados da amostra um modelo de regressão linear do salário (Y, em mil reais) em função do tempo de experiência no cargo (x, em anos), obtendo a equação estimada 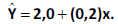. A estimativa de regressão para o salário médio é

• A. 2,0 + (0,2)(4).
• B. 2,0 + (0,2)(6).
• C. 2,0 + (0,2)(8).
• D. 3,6 + (0,2)(4).
• E. 3,6 + (0,2)(8).

Uma cidade tem 12.000 domicílios divididos em três bairros (denotados por B1, B2 e B3), que pagam IPTU em três faixas de valores (denotadas por I1, I2 e I3). Sabe-se que um pesquisador deseja estimar a média da renda mensal destes domicílios via Amostragem Estraficada ou Amostragem por Conglomerados de 1.200 domicílios. O quadro a seguir mostra o número de domicílios e a variância da renda mensal em cada faixa de IPTU e em cada bairro. A variância da renda mensal entre todos os domicílios da região é igual a 3.400 (variância global).

Com o objetivo de aumentar a precisão do estimador da média da renda mensal, é correto afirmar que

• A. a variável “bairro” é a mais adequada para formação de estratos, pois os três bairros têm número de domicílios iguais.
• B. a variável “bairro” é a mais adequada para formação de conglomerados, pois os três bairros têm número de domicílios iguais.
• C. a variável “IPTU” é a mais adequada para formação de estratos, pois suas três faixas têm número de domicílios diferentes.
• D. a variável “bairro” é a mais adequada para formação de estratos, pois a variabilidade da renda domiciliar dentro de cada bairro é próxima da variabilidade global.
• E. a variável “IPTU” é a mais adequada para formação de estratos, pois a variabilidade da renda domiciliar dentro de cada faixa de IPTU é menor do que a variabilidade global.

Uma equipe de pesquisas deseja avaliar uma nova técnica de aprendizagem. Para isso, dispõe de um grupo com 124 voluntários, submetidos ao seguinte experimento: de uma lista de 60 termos sobre determinado assunto, cada voluntário deveria registrar o número de termos para os quais ele conhecia o significado. Após essa primeira medição do conhecimento dos voluntários, o grupo foi submetido a uma sessão que utilizava a técnica de aprendizagem em avaliação. Logo após a sessão, os voluntários deveriam olhar a mesma lista de 60 termos utilizada anteriormente e registrar novamente o número de termos para os quais eles conheciam o significado. A suspeita da equipe de pesquisa é a de que o número de termos conhecidos aumente depois da sessão que utiliza a técnica em avaliação. Considerando apenas o desenho do experimento e a variável utilizada para medir o conhecimento dos voluntários (outras suposições serão verificadas posteriormente), o conjunto de testes estatísticos que podem ser usados para verificar a suspeita da equipe é

• A. Teste de Mann-Whitney, Teste de Walsh, Teste do Sinal, Teste t-Student.
• B. Teste do Sinal, Teste de Walsh, Teste de Kruskal-Wallis, Teste de McNemar.
• C. Teste t-Student, Teste de Kruskal-Wallis, Teste do Sinal, Teste de McNemar.
• D. Teste de Mann-Whitney, Teste de Walsh, Teste do Sinal, Teste de Kruskal-Wallis.
• E. Teste t-Student, Teste de Walsh, Teste do Sinal, Teste de Wilcoxon dos Postos Sinalizados.

Uma indústria mineradora produz minério de ferro e tem um contrato com uma siderúrgica, especificando que o teor médio de ferro nos lotes de minério entregue a ela deve ser de, no mínimo, 60%. Caso contrário, os lotes são devolvidos e a mineradora deve pagar uma multa. Para certificar-se de que está enviando minério de ferro dentro do que foi especificado no contrato, a mineradora toma amostras de minério de cada lote a ser embarcado. Em seguida, determina o teor médio de ferro do minério de cada lote. A mineradora gostaria que a probabilidade de concluir o lote a ser enviado cumprisse as especificações estabelecidas pela siderúrgica quando, na verdade, não as cumpre, seja, no máximo, 0,025. Considere as quatro hipóteses a seguir:

Hipótese 1: o teor médio de minério de ferro do lote é maior do que 60%.

Hipótese 2: o teor médio de minério de ferro do lote é maior ou igual a 60%.

Hipótese 3: o teor médio de minério de ferro do lote é menor do que 60%.

Hipótese 4: o teor médio de minério de ferro do lote é menor ou igual a 60%.

Considerando as informações apresentadas, as hipóteses nulas e a alternativa do teste a ser realizada antes do embarque do lote são, respectivamente, as hipóteses

• A. 3 e 1.
• B. 4 e 1.
• C. 2 e 3.
• D. 1 e 3.
• E. 1 e 4.

Uma indústria de confecções suspeita que as peças de tecido recebidas de uma fábrica, ao longo dos cinco dias da semana, não são homogêneas quanto à resistência das fibras à tensão depois da tintura. Para verificar essa suspeita, uma amostra de 9 peças de tecido de cada um dos cinco dias da semana foi avaliada quanto à resistência das fibras à tensão depois da tintura. Os resultados da análise apropriada e aplicada a esses dados estão resumidos na tabela a seguir.

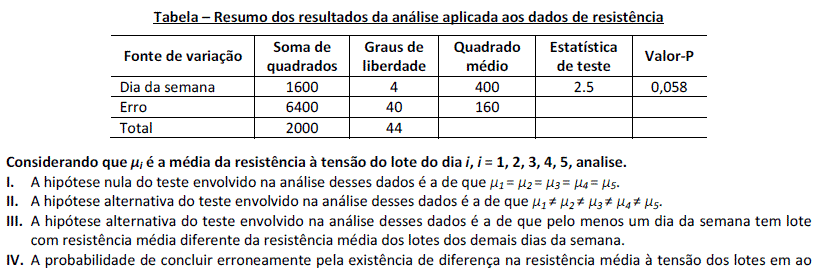
Está(ão) correta(s) apenas a(s) afirmativa(s)

• A. I.
• B. I e II.
• C. I e III.
• D. I, II e IV.
• E. I, III e IV.

Um analista dispõe dos valores da média aritmética simples, da mediana e do desvio-padrão da idade de dois grupos de 100 eleitores, um do sexo feminino e outro do sexo masculino. Para o grupo feminino, os valores são: média igual a 56 anos, mediana igual a 52 anos e desviopadrão igual a 5 anos. Para o grupo do sexo masculino, os valores são: média igual a 60 anos, mediana igual a 58 anos e desvio-padrão igual a 7 anos. O analista gostaria de conhecer as estatísticas descritivas para a idade no grupo total de 200 eleitores, mas só dispõe das estatísticas separadas por sexo, cujos valores são os mencionados anteriormente. Sobre o problema citado anteriormente, analise as afirmativas.

I. A média da idade do grupo total de eleitores pode ser obtida a partir das médias de idades dos grupos separados por sexo e o seu valor é 58 anos.

II. O desvio-padrão da idade do grupo total de eleitores pode ser obtido a partir dos desvios-padrão das idades dos grupos separados por sexo e o seu valor é 6 anos.

III. A mediana da idade do grupo total de eleitores pode ser obtida a partir das medianas das idades dos grupos separados por sexo e o seu valor é 55 anos.

Está(ão) correta(s) a(s) afirmativa(s)

• A. I, II e III.
• B. I, apenas.
• C. II, apenas.
• D. III, apenas.
• E. I e III, apenas.